
|
Solving Systems of Equations |
| 1. |
Solve
the linear system: y = -2x + 9
and y = 3x - 4
|
| |
a. (non-graphical approach)
1.  Document #1 New , #1 Add Calculator Document #1 New , #1 Add Calculator
2.  , #3 Algebra, #2 Solve System of Linear Equations , #3 Algebra, #2 Solve System of Linear Equations
Number of equations: 2
Variable: x,y
OK
3. Enter the equations in the boxes.
4. Hit 
|


Conversion to decimal not required.
|
| |
|
| |
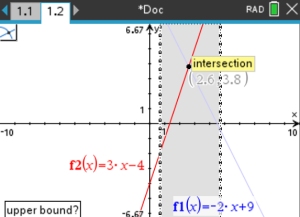
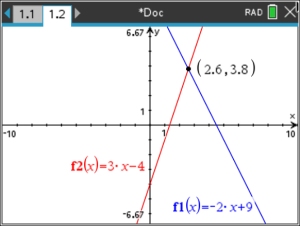
b. (graphical approach)
1.  Document #1 New , #1 Add Graph Document #1 New , #1 Add Graph
2. Graph the two equations.
Hit
 between entries to return to entry area. between entries to return to entry area.
3.  , #6 Aanaylze Graph, , #6 Aanaylze Graph,
#4 Intersection
Scroll and lock upper and lower bounds surrounding the intersection point.
4. Intersection cordinates appear.
5. ANSWER: (2.6, 3.8)
|
|
|
| 2. |
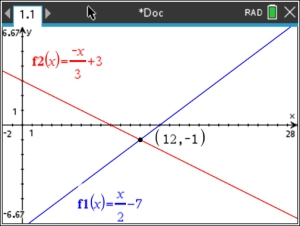
Solve
the linear system: x - 2y = 14
and x + 3y = 9
|
| |
The graphing calculator will only accept
function entries that start with "f (x) =",
( "y = " ),
so we need
to solve these equations for"y =".
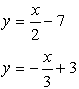
1. Enter the first equation into f1(x). 
 to access f2(x), to access f2(x),
2. Enter the second equation into f2(x). 
3. Adjust the Window to show the intersection point if needed.
 , #4 Window/Zoom, #1 Window Settings , #4 Window/Zoom, #1 Window Settings
4. Find intersection point.
 , #6 Aanaylze Graph, , #6 Aanaylze Graph,
#4 Intersection
Scroll and lock upper and lower bounds surrounding the intersection point.
5. ANSWER: (12, -1) |
Graph functions:
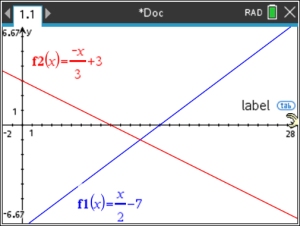
Oops!!
 |
|
| 3. |
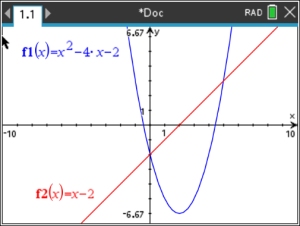
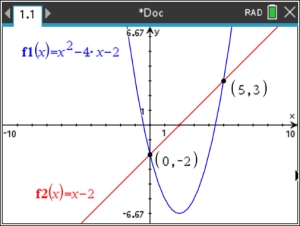
Solve
linear quadratic system: y = x2 - 4x - 2 and y = x - 2
|
| |
1. Enter the first equation into f1(x). 

2. Enter the second equation into f2(2).
3. If needed, adjust window so intersection points are veiwable on the screen.
 , #4 Window/Zoom, #1 Window Settings , #4 Window/Zoom, #1 Window Settings
4. Use the INTERSECTION option
twice to find the
two locations where the graphs intersect.
 , #6 Aanaylze Graph, , #6 Aanaylze Graph,
#4 Intersection
Scroll and lock upper and lower bounds surrounding the intersection point. .
5.
Answer: (5,3)
and (0,-2)
|
|
|
|
| 4. |
Solve 3 x 3 linear system:
(non-graphical approach)
|
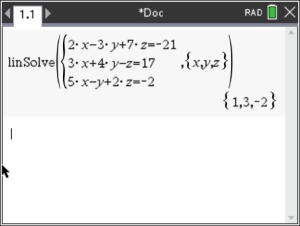
2x - 3y + 7z = -21
3x + 4y - z = 17
5x - y + 2z = -2
|
| |
1.  Document #1 New , #1 Add Calculator Document #1 New , #1 Add Calculator
2.  , #3 Algebra, #2 Solve System of Linear Equations , #3 Algebra, #2 Solve System of Linear Equations
Number of equations: 3
Variable: x,y,z
OK
3. Enter the equations in the boxes.
4. Hit 
5.
Answer: (1, 3, -2)
|

|
| |
 |
| |
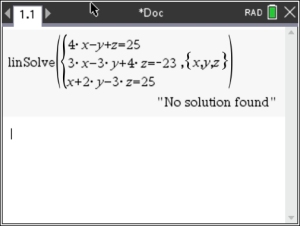
There is the possibility of NO SOLUTION:
The calculator will report
"No solution found" when this occurs.
 |
There is also the possibility of
AN INFINITE NUMBER of solutions.
The calculator will show a variable, cl, in the solution, indicating any value can be substituted into that variable. 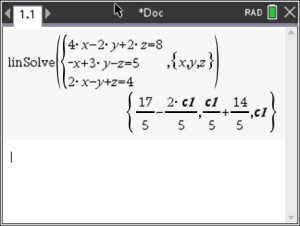 |
|

Table of Contents | MathBits.com | Terms of Use
|
|

